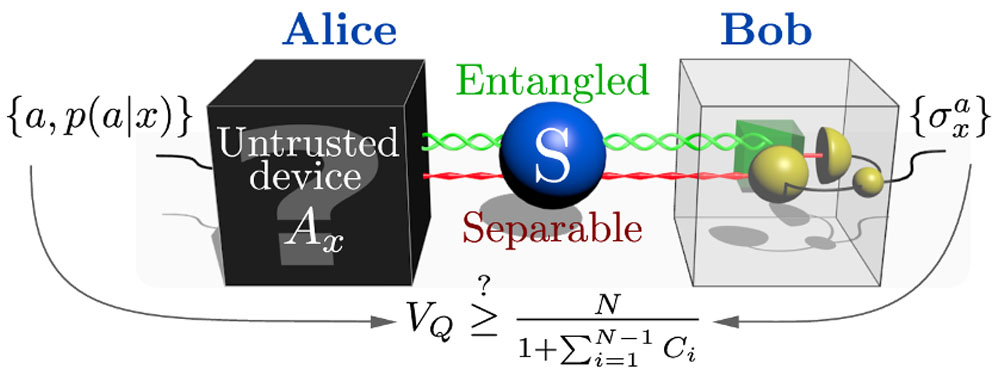
Schemat eksperymentalnego testowania nierówności sterowania kwantowego [2]
Ważnym filarem rozwoju technologii kwantowych jest teoria informacji kwantowej, która opisuje jak dane zakodowane w kwantowych bitach (qubitach) są przechowywane, przetwarzane i przesyłane. Odpowiada ona na pytania dotyczące urządzeń kwantowych: jakie operacje i algorytmy można z ich pomocą zrealizować, jak zakodować dane na wejściu i jak zinterpretować rezultaty. Podsumowując, teoria informacja kwantowej daje nam wiedzę jak można praktycznie skorzystać z potężnych możliwości wynikających z praw mechaniki kwantowej do np. przeprowadzenia odpornej na podsłuch transmisji danych, uzyskania prawdziwie losowych liczb potrzebnych w informatyce albo zwiększenia precyzji pomiarów ponad ograniczenia wynikające z fizyki klasycznej.
Nasze badania prowadzimy w odniesieniu do rzeczywistych układów eksperymentalnych i aparatury dostępnej w laboratoriach. Najbardziej rozpowszechnione źródła światła kwantowego działają w oparciu o zjawisko parametrycznego podziału częstości (ang. parametric down-conversion, PDC), które występuje w nieliniowych kryształach takich jak PPLN (periodycznie spolaryzowany nioban litu) lub PPKTP (periodycznie spolaryzowany fosforan tytanowo-potasowy). Wytwarzają one wielofotonowy stan ściśniętej próżni. W połączeniu z nowoczesną optyką zintegrowaną oraz detektorami zliczającymi fotony wykorzystującymi zjawisko nadprzewodnictwa, np. TES (ang. Transition-Edge Sensors), stanowią one kluczową platformę dla aplikacji kwantowych. Dlatego warto jest badać jej możliwości.
Naszym osiągnięciem jest zaproponowanie nowych metod badania korelacji kwantowych, które są szczególnie dobrze dopasowane do możliwości współczesnej aparatury. Są to nowoczesne narzędzia, które pozwalają wdrożyć technologie kwantowe z jednoczesnym samotestowaniem urządzeń.
Opracowaliśmy łańcuchowe nierówności Bella dopasowane specjalnie dla wielofotonowego stanu splątanej próżni [1], który można w przybliżeniu opisać jako dwie kopie stanu EPR (Einsteina-Podolsky’ego-Rosena). Nierówności te oparte są na koncepcji odległości i uogólnionej nierówności trójkąta. W teście Bella, dwóch oddalonych obserwatorów wykonuje lokalne pomiary liczby fotonów w różnych bazach polaryzacji. W artykule zaproponowano protokół, w którym obserwatorzy zmieniają ustawienia tak, że kąt względny między polaryzatorami jest stały i odwrotnie proporcjonalny do liczby pomiarów. Zwiększanie tej liczby prowadzi do argumentu typu Greenbergera-Horne’a-Zeilingera (GHZ), w którym mechanika klasyczna przewiduje istnienie idealnych korelacji między pomiarami u obu obserwatorów, natomiast kwantowa – antykorelacji, co powoduje łamanie nierówności. Pokazaliśmy, że nasz test Bella jest już obecnie wykonalny w laboratoriach dla stanów wielofotonowych, dla niewielkiej liczby ustawień pomiarowych oraz dla niedużego wzmocnienia parametrycznego, także przy stratach obecnych w systemie. Przykładowo, w przypadku stanu wielofotonowej ściśniętej próżni wytworzonej przy wzmocnieniu parametrycznym 0.6 (co odpowiada średniej liczbie fotonów 0.81), możliwe jest przeprowadzenie testu z użyciem zaledwie 5 pomiarów i detektorów TES.
Kwantowe sterowanie reprezentuje inny, słabiej zbadany typ korelacji kwantowych niż nielokalności Bella. Pozwala na łatwiejszą realizację testu, jest więc bardzo interesujące z punktu widzenia eksperymentalnego. Można za jego pomocą przeprowadzać testy urządzeń kwantowych przy założeniu, że część z nich działa poprawnie. W protokole tym obserwator dokonując pomiaru jednej ze splątanych cząstek wpływa na stan cząstki u drugiego obserwatora – steruje nią. Dotychczasowe podejścia wymagały jednak, aby liczba pomiarów szybko rosła wraz z rosnącym wymiarem układu (liczbą cząstek) co w praktyce uniemożliwiało stosowanie go w przypadku np. wielofotonowych stanów światła. W artykule [2] opisaliśmy nowy, odporny na niedoskonałości układu doświadczalnego protokół kwantowego sterowania, oparty na uogólnieniu pomiarów wykonywanych we wzajemnie nieobciążonych bazach (ang. mutually ubiased bases). W odróżnieniu od dotychczas stosowanych metod, nasze podejście pozwala na przeprowadzanie eksperymentów z użyciem dostępnych technik pomiarowych i liczby ustawień która prawie nie zmienia się wraz z rosnącym wymiarem, co umożliwia ich praktyczną realizację. Zaproponowaliśmy implementację z użyciem wielofotonowych stanów wytworzonych za pomocą źródła PDC oraz pomiarów zliczających fotony i pokazaliśmy jak dla nich dobrać optymalne ustawienia (Rys. 1). Przykładowo, dla stanu składającego się z 6 fotonów, wystarczą N = 3 ustawienia.
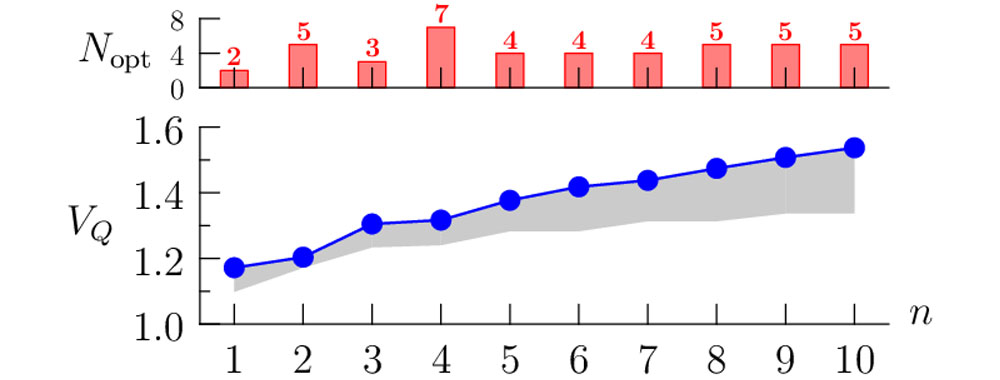
Rys. 1. Łamanie nierówności kwantowego sterowania VQ oraz optymalna liczba ustawień Nopt dla wielofotonowego stanu ściśniętej próżni o 2n cząstkach
[2] K. Rosołek, M. Stobińska, M. Wieśniak, M. Żukowski, Two Copies of the Einstein-Podolsky-Rosen State of Light Lead to Refutation of EPR Ideas, Phys. Rev. Lett. 114, 100402 (2015).
PDF
[3] A. Rutkowski, A. Buraczewski, P. Horodecki, M. Stobińska, Quantum Steering Inequality with Tolerance for Measurement-Setting Errors: Experimentally Feasible Signature of Unbounded Violation, Phys. Rev. Lett. 118, 020402 (2017).
PDF


