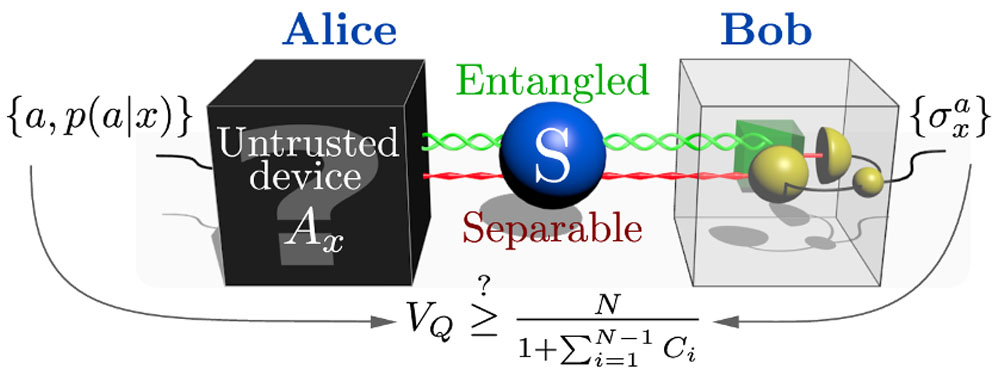
Experimental scheme for testing the quantum steering inequality violation [2]
Quantum information theory is one of the pillars underlying the development of quantum technologies. It explains how the data encoded in quantum bits (qubits) is stored, processed and transmitted. This theory answers many important questions regarding quantum devices: what operations and algorithms can be implemented, in what way the information should be encoded and how to interpret the results. Summarizing, the quantum information theory enables building knowledge about practical applications of powerful capabilities resulting from the laws of quantum mechanics. It allows us to e.g. develop information transmitters resistant to eavesdropping, generate truly random numbers required in information technologies as well as to increase precision of measurements over the limit imposed by classical physics.
The research performed by our Group is related to realistic capabilities of experimental setups of the apparatus available in labs. The most widespread sources of quantum light are based on the parametric down-conversion process (PDC) which is revealed by nonlinear crystals such as PPLN (periodically-poled lithium niobate) or PPKTP (periodically-poled potassium titanyl phosphate). They are capable of generating the multiphoton state of squeezed vacuum. When merged with modern integrated optics and superconducting photon counting detectors (e.g. Transition-Edge Sensors, TESs), they constitute a core platform for quantum applications. For this reason, it is crucial to investigate its possibilities.
Our accomplishment is to propose new protocols of testing quantum correlations in the way which is well suited to the capabilities of modern quantum lab equipment. These modern tools allow to implement quantum technologies with built-in device self-testing.
We developed chained Bell inequalities tailored for the multiphoton squeezed vacuum state [1], which can be approximately described as two copies of the EPR (Einstein-Podolsky-Rosen) state. Our inequalities are built on a concept of a distance and a generalized triangle inequality. In the Bell test, two separated observers perform local photon number measurements in different polarization bases. In our paper, we proposed a protocol in which the observers change their settings so that the relative angle between the polarizers is constant and inversely proportional to the number of measurements. Growing number of settings leads to the Greenberger-Horne-Zeilinger-type (GHZ) argument, where classical physics foresees ideal correlation between measurements of both observers but quantum mechanics – anticorrelation, which leads to violation of the inequality. We showed that our test can be already performed in labs for multiphoton states, for a low number of measurement settings and a moderate value of the parametric gain, even in the presence of losses. For example, in case of multiphoton squeezed vacuum obtained with parametric gain equal to 0.6 (ca. 0.81 photons on average), it is possible to use as few as 5 measurements with TES detectors.
Quantum steering represents another, less investigated type of quantum correlations compared to Bell nonlocalities. It allows easier testing and thus, it is very interesting from the experimental point of view. It makes it possible to perform tests of quantum devices with assumption that part of them is working correctly. In this protocol the observer making the measurement of one of the entangled particles influences the state of the other particle – steers it. Previous attempts required the number of measurements to grow rapidly with the increasing dimension of the system (number of particles) which practically rendered quantum steering unfeasible in case of multiphoton states. In our paper [2] we described a new protocol which is resistant to imperfections of the experimental setup. It is founded on generalization of mutually unbiased bases measurements. In contrast to previous methods, our approach allows to perform experiments with available detection techniques and the number of settings almost constant in relation to the increasing dimension, which makes them feasible. We proposed an implementation with multiphoton states produced with the PDC source as well as photon counting measurements and showed how to choose the optimal settings (Fig. 1). For example, for a 6-photon state is enough to perform only N = 3 measurements.
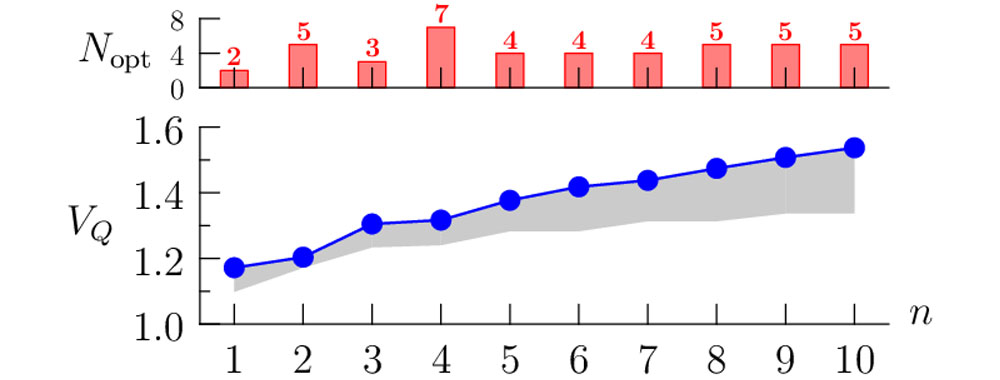
Rys. 1. Quantum steering inequality violation VQ and the optimal numer of settings Nopt for multiphoton squeezed vacuum state of 2 n particles
[2] K. Rosołek, M. Stobińska, M. Wieśniak, M. Żukowski, Two Copies of the Einstein-Podolsky-Rosen State of Light Lead to Refutation of EPR Ideas, Phys. Rev. Lett. 114, 100402 (2015).
PDF
[3] A. Rutkowski, A. Buraczewski, P. Horodecki, M. Stobińska, Quantum Steering Inequality with Tolerance for Measurement-Setting Errors: Experimentally Feasible Signature of Unbounded Violation, Phys. Rev. Lett. 118, 020402 (2017).
PDF



