What is quantum communication and what it offers?
Quantum communication uses quantum resources, such as quantum entanglement or qubits, to exchange information encoded in physical states of quantum objects. It is analogous to classical communications which is based on sending zeros and ones encoded in electronic or photonic states. One of the goals of quantum communications is to boost the protection from eavesdropping and tampering by means of quantum cryptography. It helps resolve a long-standing open problem of secure cryptographic key distribution. In a nutshell, quantum communication first, physically distributes quantum information between distant users through a quantum channel and next, enables them to perform a quantum key distribution protocol (QKD).
What is the difference between conventional and quantum cryptography?
Conventional (classical) cryptography as well as post-quantum cryptography (PQC) rely on assumptions that certain mathematical problems are computationally hard, and therefore cannot be solved in a reasonable time, in this way protecting the information. However, these assumptions may become invalid because of advances in science and technology. For example, factorization of large integers into prime numbers ? a basis of the prominent RSA algorithm ? was believed to be hard, until the invention of the Shor?s algorithm. The security of encryption schemes based on algorithms is limited by the computational power of an adversary, which may stem from a quantum computer as well as a conventional High-Performance Computer (HPC) system. Thus, these kinds of cryptographic schemes are called computationally secure.
In contrast, quantum cryptography is based on the laws of quantum mechanics. The assumptions that stand behind it are that the quantum theory is correct and complete; and quantum mechanics is the best tested physical theory. The security it offers holds even in the presence of an adversary who possesses unbounded computational resources. Therefore, it offers unconditional (information theoretic) security.
How many different types of QKD protocols are there?
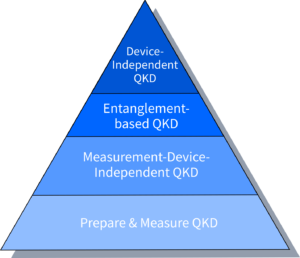
Over the years, numerous quantum key distribution protocols have been developed. They can be grouped into four classes (compare the figure): 1) Prepare & Measure QKD, 2) Measurement-Device-Independent (MDI) QKD, 3) Entanglement-based QKD, and 4) Device-Independent (DI) QKD. The highest level of security is provided by the DI QKD class, as these protocols can be safely implemented with uncharacterized, untrusted devices ? the top of quantum-enhanced security pyramid. Gradually, the lower levels correspond to higher number of assumptions on the inner workings of the devices that implement them, and thus, lower security gains.
What do we do?
Our twist on quantum communications is to pave the way to its wider adoption soon. We aim to create new solutions that are implementable with the existing quantum photonic hardware. To this end, we study limitations and performance of quantum components such as sources of quantum light and photodetection techniques, and then we design a new protocol that possesses desired features.
Providing security proof is another crucial step in our work. We use the Devetak-Winter formula which gives us the secure key rate against collective attacks and then combining it with the EAT theorem, one can prove the security against coherent attacks. To calculate the secure key rate, we either map our solutions to some already known analytical bounds which obtained from applying the Jordan lemma on Bell inequalities, or we use numerical techniques, harnessing semi-definite programming (Navascués-Pironio-Acín hierarchy).
We also employ numerous post-processing techniques that either alter the protocol slightly, such as random sampling of measurement results, or add to it advanced numerical data processing, e.g., noisy pre-processing, in order to further lower the requirements for hardware performance, photodetection efficiencies for instance, and increase the generated secret key rates.
Recently, we developed a protocol to perform long-range distribution of near-maximally entangled multiphoton states, allowing versatile applications such as quantum key distribution and quantum metrology which can provide alternatives to state-of-the-art protocols. Our scheme uses resources available within the current integrated quantum photonic technology: squeezed vacuum states and photon-number-resolving detectors. The distributed entanglement can be certified by Bell tests which have the potential to be loophole free and may be directly used in well-established QKD protocols. Generally, this provides measurement-device-independent levels of security, which may be upgraded to fully device-independent security if the Bell test is loophole free. In both cases, the protocol is robust to extremely high transmission losses, matching the optimal O(sqrt(eta)) scaling of key rate with channel transmittance.
References
- M. E. Mycroft, T. McDermott, A. Buraczewski, M. Stobińska, Proposal for the distribution of multiphoton entanglement with optimal rate-distance scaling, Phys. Rev. A 107, 012607 (2023).
- A. Rutkowski, A. Buraczewski, P. Horodecki, M. Stobińska, Quantum steering inequality with tolerance for measurement-setting-errors: experimentally feasible signature of unbounded violation, Phys. Rev. Lett. 118, 020402 (2017).
- K. Rosołek, M. Stobińska, M. Wieśniak, M. Żukowski, Two Copies of the Einstein-Podolsky-Rosen State of Light Lead to Refutation of EPR Ideas, Phys. Rev. Lett. 114, 100402 (2015).



